• 해시 테이블
  • 1 개요
  • 2 해시
    • 2.1 해시 함수
      • 2.1.1 설명
      • 2.1.2 좋은 해시 함수들의 특징
      • 2.1.3 사용례
      • 2.1.4 나눗셈 방식(Modulo-Division Method)
        • 2.1.4.1 $h(x)$
        • 2.1.4.2 $x$
        • 2.1.4.3 $m$
    • 2.2 해싱(Hashing)
      • 2.2.1 설명
      • 2.2.2 사용례
  • 3 충돌
    • 3.1 생일 문제
      • 3.1.1 설명
      • 3.1.2 실험 파이썬 코드
    • 3.2 비둘기집 원리(또는 서랍 원리)
      • 3.2.1 설명
    • 3.3 로드 팩터
      • 3.3.1 설명
    • 3.4 처리 방식
      • 3.4.1 개별 체이닝
        • 3.4.1.1 설명
        • 3.4.1.2 예제
      • 3.4.2 오픈 어드레싱
        • 3.4.2.1 설명
        • 3.4.2.2 예제
  • 4 언어별 해시 테이블 구현 방식

해시 테이블

1 개요

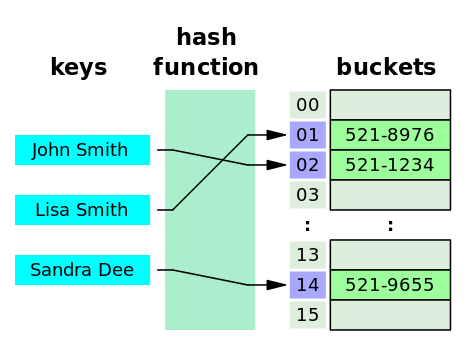
• 해시 테이블 또는 해시 맵
• 키를 값에 매핑할 수 있는 구조인, 연관 배열(associative array) 추상 자료형을 구현하는 자료 구조
• 대부분의 연산이 분할 상환 분석에 따른 시간 복잡도가 $O(1)$

2 해시

2.1 해시 함수

2.1.1 설명

• 임의 크기 데이터를 고정 크기 값으로 매핑하는 데 사용할 수 있는 함수

ABC     -해시 함수-> A1
1324BC  -해시 함수-> CB
AF32B   -해시 함수-> D5

• 최상의 분포를 제공하는 방법은 데이터에 따라 제각각

2.1.2 좋은 해시 함수들의 특징

• 해시 함수 값 충돌의 최소화
  • 고정 크기 값으로 변환하면서 같은 값이 나올 수 있기 때문
• 쉽고 빠른 연산
• 해시 테이블 전체에 해시 값이 균일하게 분포
• 사용할 키의 모든 정보를 이용하여 해싱
  • 최대한 겹치지 않도록
• 해시 테이블 사용 효율이 높을 것

2.1.3 사용례

• 개념이 겹치거나 혼용되긴 하지만, 용도와 요구 사항에 따라 각각 다르게 설계되고 최적화된다
  • 체크섬(Checksum)
  • 손실 압축
  • 무작위화 함수(Randomization Function)
  • 암호

2.1.4 나눗셈 방식(Modulo-Division Method)

• $h(x) = x \mod m$

2.1.4.1 $h(x)$

• 해시 함수의 결과

2.1.4.2 $x$

• 어떤 간단한 규칙 통해 만들어낸 충분히 랜덤한 상태의 키의 값
• 조슈아 블로크는 자바 설계 시 값 x를 다항식의 결과로 정의

• 여기서 $x$는 31로 하는 거듭제곱 $P(31)$의 연산으로 정의
• 여러 해시 함수의 성능을 조사했고, The C Programming Language에서 P(31)을 찾아냈다. 이 값은 97년 당시 RISC 머신에서 가장 저렴한 계산 비용이 들었다고 한다

unsigned hash(char *s){
    unsigned hashval;

    for (hashval = 0; *s != '\0'; s++)
        hashval = *s + 31 * hashval;

    return hashval % HASHSIZE;
}

• JDK에 포함된 해시 코드 중 일부

hashCode = 31 * hashCode + (e == null ? 0 : e.hashCode());

2.1.4.3 $m$

• 해시 테이블의 크기

2.2 해싱(Hashing)

2.2.1 설명

• 해시 테이블을 인덱싱하기 위해 해시 함수를 사용하는 것
• 정보를 가능한 한 빠르게 저장하고 검색하기 위해 사용하는 중요한 기법 중 하나

2.2.2 사용례

• 최적의 검색이 필요한 분야
• 심볼 테이블 등의 자료구조 구현

3 충돌

• John Smith와 Sandra Dee의 해시 결과(152)가 충돌

3.1 생일 문제

3.1.1 설명

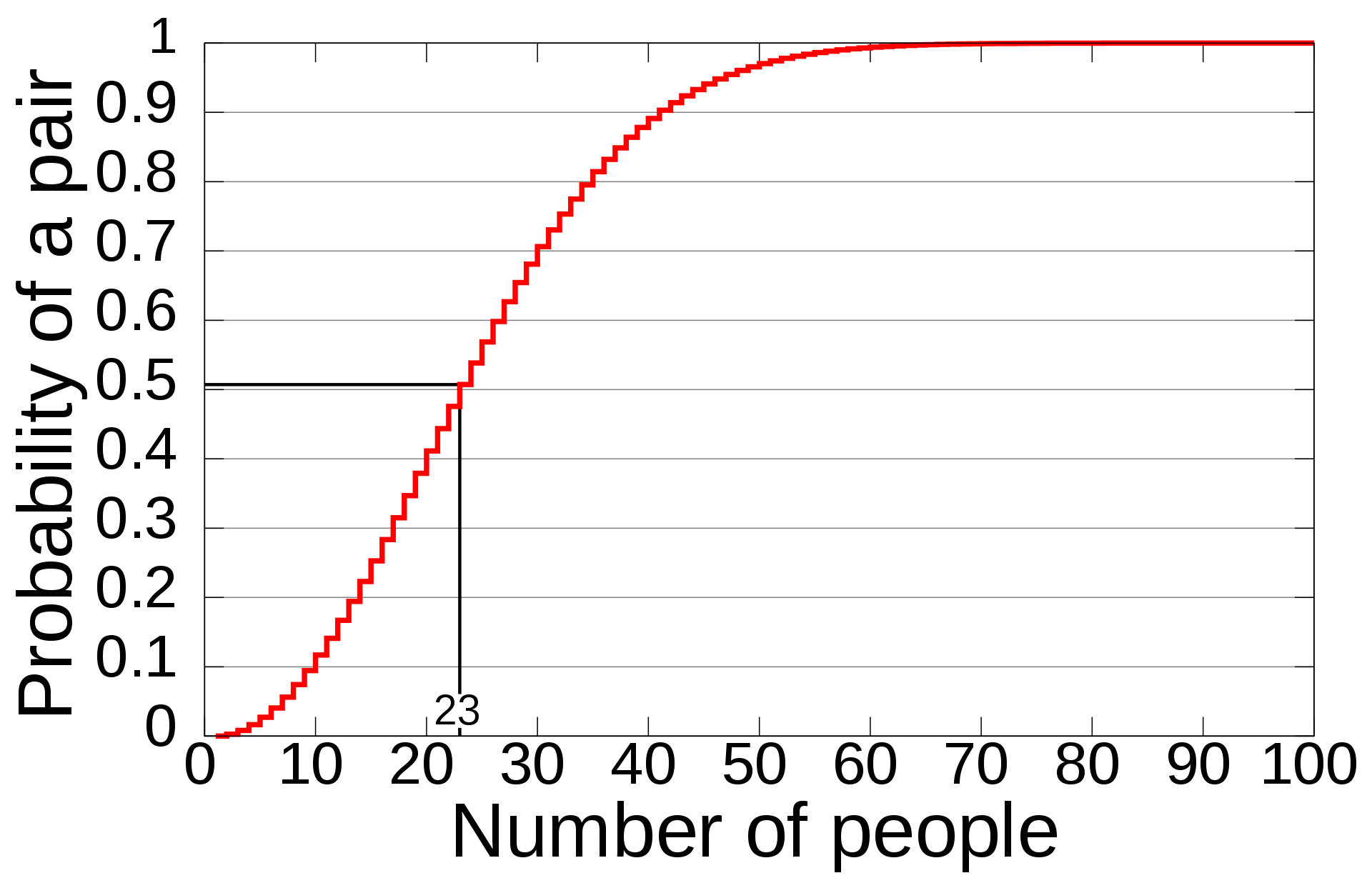
여러 사람이 모였을 때 생일이 같은 2명이 존재할 확률은, 23명만 모여도 50%를 넘고, 57명 모이면 99%를 넘는다

3.1.2 실험 파이썬 코드

import random

TRIALS = 100000
same_birthday = 0.0

for _ in range(TRIALS):
    birthdays = []
    for i in range(23):
        birthday = random.randint(1, 365)
        if birthday in birthdays:
            same_birthday += 1
            break
        birthdays.append(birthday)

print(f'{same_birthday / TRIALS * 100}%')  # 50.88399999999999%

3.2 비둘기집 원리(또는 서랍 원리)

3.2.1 설명

n개 아이템을 m개 컨테이너에 넣을 때, n > m이라면 적어도 하나의 컨테이너에는 반드시 2개 이상의 아이템이 들어있다

• 9개 아이템을 10개 컨테이너에 넣을 때, 반드시 1번 이상은 충돌이 발생
  • 좋은 해시 함수라면 1번의 충돌
  • 나쁜 해시 함수라면 9번의 충돌

3.3 로드 팩터

3.3.1 설명

해시 테이블에 저장된 데이터 개수 n을 버킷의 개수 k로 나눈 것

• 로드 팩터 비율에 따라
  • 해시 함수 재작성
  • 또는 해시 테이블 크기 조정 결정
• 해시 함수가 키들을 잘 분산해주는지를 말하는 효율성 측정에도 사용
• $\text{로드 팩터 증가} = \text{버킷당 저장되는 데이터 개수 증가} \to \text{해시 테이블 성능 감소}$

3.4 처리 방식

3.4.1 개별 체이닝

3.4.1.1 설명

• 해시 테이블의 기본 방식
• 충돌 발생 시 연결 리스트로 연결(link) 하는 방식
• 사실상 무한정 저장 가능
• C++(GCC libstdc++), Java, Go

3.4.1.2 예제

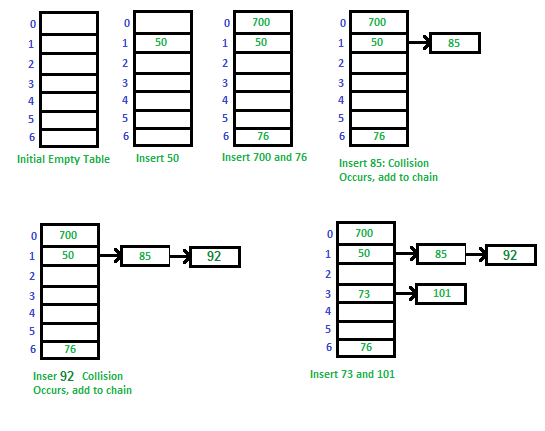
1. 테이블 초기화
2. 50 입력
3. 700과 76 입력
4. 85 입력 시 50과 충돌 발생 $\to$ 체인 추가
5. 92 입력 시 50과 충돌 발생 $\to$ 체인 추가
6. 73과 101 입력, 101에서 충돌 발생 $\to$ 체인 추가

3.4.2 오픈 어드레싱

3.4.2.1 설명

• 충돌 발생 시 테이블 공간 내에서 탐사를 통해 빈 공간을 찾아서 해결
• 전체 슬롯 개수 이상 저장 불가
• 모든 원소가 반드시 자신의 해시값과 일치하는 주소에 저장된다는 보장은 없다
• Python, Ruby

3.4.2.2 예제

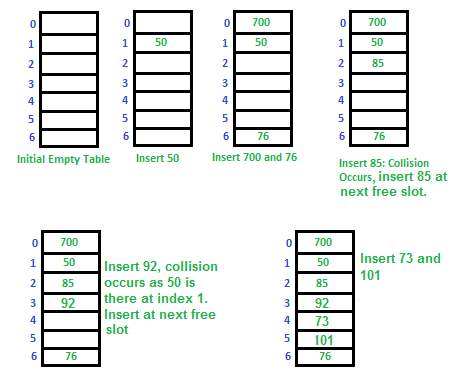
1. 테이블 초기화
2. 50 입력
3. 700과 76 입력
4. 85 입력 시 50과 충돌 발생 $\to$ 다음 빈 슬롯에 입력
5. 92 입력 시 50과 충돌 발생 $\to$ 다음 빈 슬롯에 입력
6. 73과 101 입력

4 언어별 해시 테이블 구현 방식