그래프
개요
- 그래프?
- 객체의 일부 쌍(pair)들이 연관되어 있는 객체 집합 구조
- 위상수학(Topology)?
- 연속변환(continuous transformation)에 대해?
- 불변인?
- 기하학적 객체?
- 특성을 연구
오일러 경로
모든 간선(edge)을 한 번씩 방문하는 유한 그래프(Finite Graph).
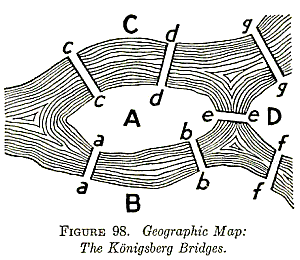
- A ~ D: 정점(vertex)
- a ~ g: 간선(edge)
- 오일러 정리(Euler’s Theorem): 모든 정점(vertex)이 짝 수 개의 차수(degree)를 갖는다면 모든 다리를 한 번씩만 건너서 도달하는 것이 성립
- 오일러 경로(Eulerian Trail):
- 간선(edge)을 기준으로 한다
해밀턴 경로
각 정점을 한 번씩 방문하는 무향 또는 유향 그래프 경로.
- 해밀턴 경로(Hamiltonian Path):
- 정점(vertex)을 기준으로 한다
- 최적 알고리즘 없는 대표적인 NP-완전 문제
- 해밀턴 순환(Hamiltonian Cycle):
- 해밀턴 경로에서 원래 출발점으로 돌아오는 경로
- 외판원 문제:
- 해밀턴 순환에서 가장 짧은 경로
그래프 순회
그래프 탐색(Search). 그래프의 각 정점을 방문하는 과정.
그래프 표현 방식
인접 행렬(Adjacency Matrix)
graph = {
1 2 3 4 5 6 7
1:[0, 1, 1, 1, 0, 0, 0],
2:[0, 0, 0, 0, 1, 0, 0]
3:[0, 0, 0, 0, 1, 0, 0]
4:[0, 0, 0, 0, 0, 0, 0]
5:[0, 0, 0, 0, 0, 1, 1]
6:[0, 0, 0, 0, 0, 0, 0]
7:[0, 0, 1, 0, 0, 0, 0]
}
인접 리스트(Adjacency List)
- 출발 노드: key, 즉 딕셔너리의 키
- 도착 노드: value, 즉 딕셔너리의 키가 가리키는 배열
graph = {
1: [2, 3, 4],
2: [5],
3: [5],
4: [],
5: [6, 7],
6: [],
7: [3],
}
DFS(Depth First Search)
- 대부분의 그래프 탐색은 DSF로 구현하게 된다
- 백트래킹 통해 뛰어난 효용 보인다
DFS - 재귀
DFS(G, v)
# v(vertex, 정점)에 방문 표시
label v as discovered ''' 1. 방문 표시 '''
# 정점 v에서 v와 인접한 정점 w로 이어지는 모든 방향 있는(directed) 간선에 대해
for all directed edges from v to w that are in G.adjacentEdges(v) do
# w에 방문 표시(label)가 없다면
if vertex w is not labeled as discovered then
# 정점 w에 대한 재귀 호출
recursively call DFS(G, w)
def recursive_dfs(v, discovered = []):
discovered.append(v) ''' 1. 방문 표시 '''
for w in graph[v]:
if not w in discovered:
discovered = recursive_dfs(w, discovered)
return discovered
DFS - 반복(스택)
DFS-iterative(G, v)
# 스택 생성
let S be a stack
# 스택에 최초 미방문 정점 삽입
S.push(v)
while S is not empty do
v = S.pop()
# 현재 정점 v가 방문 표시 되지 않았다면
if v is not labeled as discovered then
# 현재 정점 v에 방문 표시 하고
label v as discovered ''' 1. 방문 표시 '''
# 정점 v에서 v와 인접한 정점 w로 이어지는 모든 간선 대해
for all edges from v to w in G.adjacentEdges(v) do
# 방문 체크 위해 스택에 삽입
S.push(w)
def iterative_dfs(start_v):
discovered = []
stack = [start_v]
while stack:
v = stack.pop()
if v not in discovered:
discovered.append(v) ''' 1. 방문 표시 '''
for w in graph[v]:
stack.append(w)
return discovered
BFS(Breadth-First Search)
- 주로 큐로 구현
BFS - 반복(큐)
BFS(G, start_v)
# Q를 큐로 선언
let Q be a queue
# start_v 방문 표시
label start_v as discovered ''' 1. 방문 표시 '''
# Q에 삽입(선입선출)
Q.enqueue(start_v)
while Q is not empty do
v := Q.dequeue()
# v가 목적지인 경우 v 리턴
if v is the goal then
return v
# v가 목적지가 아닌 경우, 노드 v에서 v에 인접한 노드 w의 모든 간선에 대하여 반복
for all edges from v to w in G.adjacentEdges(v) do
# 노드 w를 방문한 적 없다면
if w is not labeled as discovered then
# 노트 w 방문 표시
label w as discovered ''' 2. 방문 표시 '''
# w의 부모 노드를 v로 붙이고
w.parent := v
# w를 큐에 삽입하여 다음 반복문에서 목적지인지 검증한다
Q.enqueue(w)
def iterative_bfs(start_v):
discovered = [start_v] ''' 1. 방문 표시 '''
queue = [start_v]
while queue:
v = queue.pop(0)
for w in graph[v]:
if not w in discovered:
discovered.append(w) ''' 2. 방문 표시 '''
queue.append(w)
return discovered
BFS - 재귀
- 재귀로 동작하지 않는다
백트래킹
해결책에 대한 후보를 구축해 나아가다 가능성 없다고 판단되는 즉시 후보를 포기(backtrack)해 정답을 찾아가는 범용적인 알고리즘
- 제약 충족 문제(Constraint Satisfaction Problems)에 특히 유용
- 탐색을 하다가 더 갈 수 없으면 왔던 길을 되돌아가 다른 길을 찾는다는 데서 유래
- DFS와 같은 방식으로 탐색하는 모든 방법을 의미하며, DFS는 백트래킹의 골격을 이루는 알고리즘
- 주로 재귀로 구현
- 트리의 가지치기(Pruning)이라고 하며, 트리의 탐색 최적화 문제와도 관련이 깊다
제약 충족 문제(Constraint Satisfaction Problems, CSP)
수많은 제약 조건(constraints)을 충족하는 상태(states)를 찾아내는 수학 문제를 일컫는다
- 합리적인 시간 내에 문제 풀기 위해 휴리스틱과 조합 탐색 같은 개념을 함께 결합해 문제를 풀이
- 스도쿠, 십자말 풀이, 8퀸 문제, 4색 문제, 배낭 문제, 푼자열 파싱, 조합 최적화 문제 등
- 가령 스도쿠의 경우
- 제약 조건 충족: 1에서 9까지 숫자를 한 번만 넣는
- 상태: 정답
용어
정점
- 그래프의 각 노드
간선
- 노드와 노드를 잇는 선
차수
- 정점에 부속되어 있는 간선의 수