최단 경로 문제
개요
각 간선의 가중치 합이 최소가 되는 두 정점(또는 노드) 사이의 경로를 찾는 문제
- 용어
- 정점(vertex): 교차로
- 간선(edge): 길
- 가중치(weight): 이동 비용
- 그래프의 종류와 특성에 따라 다양한 최단 경로 알고리즘 존재. 가장 유명한 것은 다익스트라 알고리즘
다익스트라 알고리즘
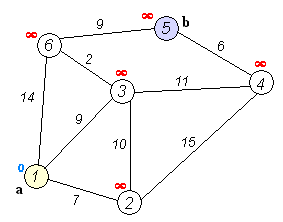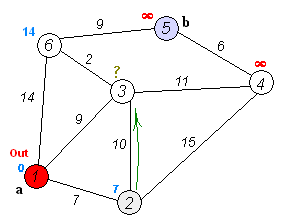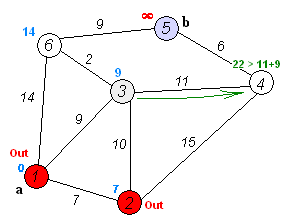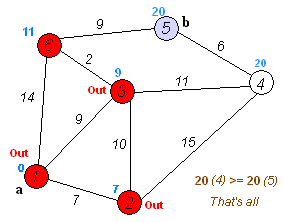
코드
function Dijkstra(Graph, source):
create vertex set Q
# 초기화
for each vertex v in Graph:
# 소스에서 v까지의 아직 모르는 길이는 무한으로 설정. 실제 무한은 아니고, 아직 방문하지 않았음을 의미.
dist[v] = INFINITY
# 소스에서 최적 경로의 이전 꼭짓점
prev[v] = UNDEFINED
# 모든 노드는 초기에 Q에 속해있다 (미방문 집합)
add v to Q
# 소스에서 소스까지의 길이
dist[source] = 0
while Q is not empty:
# 최소 거리를 갖는 꼭짓점을 가장 먼저 선택하고 제거(우선순위 큐 사용)
u = vertex in Q with min dist[u]
remove u from Q
# v는 Q에 남아 있는 정점으로, 최소 거리 갖는 현재 노드의 인접 노드들
for each neighbor v of u:
# v 까지의 더 짧은 경로를 찾았을 때
alt = dist[u] + length(u, v)
if alt < dist[v]:
# 다음 인점 노드 v까지의 거리
dist[v] = alt
# v 이전 노드 업데이트
prev[v] = u
return dist[], prev[]
설명
- 항상 노드 주변의 최단 경로만을 택하는 대표적인 그리디(Greedy) 알고리즘 중 하나
- 노드 주변 탐색 시 BFS 이용하는 대표적인 알고리즘
- 여러 갈림길을 탐색하며 가장 먼저 도착한 길을 선택
- 하지만 가중치가 음수인 경우는 처리할 수 없다
- heap?
- 완전 이진 트리의 일종.
- 우선순위 큐를 위해 만들어진 자료 구조
- max heap: 부모 노드의 키 값 >= 자식 노드의 키 값
- min heap: 부모 노드의 키 값 <= 자식 노드의 키 값
단점
- 임의의 정점을 출발 집합에 더할 때, 그 정점까지의 최단 거리는 계산이 끝났다는 확신을 갖고 더한다.
- 만일 이후에 더 짧은 경로가 존재한다면 다익스트라 알고리즘의 논리적 기반이 무너진다.
- 모두 값을 더해서 양수로 변환하는 방법
- 벨만-포드 알고리즘 같은 음수 가중치 계산할 수 있는 다른 알고리즘 사용
- 최장 거리 구하는 데에는 사용 불가
A* 알고리즘
- SebLague/Pathfinding 코드 내용을 분석하며 공부
Episode 1 - pseudocode
OPEN //the set of nodes to be evaluated
CLOSED //the set of nodes already evaluated
add the start node to OPEN
loop
current = node in OPEN with the lowest f_cost
remove current from OPEN
add current to CLOSED
if current is the target node //path has been found
return
foreach neighbour of the current node
if neighbour is not traversable or neighbour is in CLOSED
skip to the next neighbour
if new path to neighbour is shorter OR neighbour is not in OPEN
set f_cost of neighbour
set parent of neighbour to current
if neighbour is not in OPEN
add neighbour to OPEN
OPEN:- 평가될 노드 집합
CLOSED:- 이미 평가된 노드 집합
current:OPEN에서f_cost가 가장 작은 노드OPEN에서 제거하고,CLOSED에 추가
current가target이면 종료