heapq

heapq

heapq.py 내의 설명

• 최소 힙(min heap) 자료 구조로, 가장 작은 값은 언제나 0번 인덱스에 위치
• 모든 원소 k에 대하여, a[k]의 값은 항상 a[2 * (k + 1)]과 a[2 * (k + 2)]보다 작거나 같도록 유지하는 배열
• 비교를 위해, 존재하지 않는 요소는 무한으로 간주한다

# 아래 숫자는 k를 의미하며, a[k]가 아니다
                                0
              1                                 2
      3               4                5               6
  7       8       9       10      11      12      13      14
15 16   17 18   19 20   21 22   23 24   25 26   27 28   29 30

• k는 항상 $(2 \times k) + 1$과 $(2 \times k) + 2$ 상위에 위치한다
• 힙에서의 트리는 스포츠에서의 토너먼트와 비슷하다
  • 상위에 위치한 숫자는 승자고, 아래에 위치한 숫자는 상대로 볼 수 있다
    • 한 셀과 그 하위의 두 셀은 서로 다른 항목을 갖고(a[k] != a[2*k+1] != a[2*k+2])
    • 상위 셀이 두 하위 셀을 이긴다(win)
• 힙의 불변성이 항상 지켜진다면, 0번 인덱스가 최종적으로 승리하게 된다
• 기존 승자를 제거하고 다음 승자를 찾는 가장 간단한 알고리즘은,
  • 패자(예를 들어 30)를 0번 인덱스 위치로 옮긴 후
  • 힙의 불변성이 다시 성립할 때까지 새로운 0번 인덱스 밑의 트리를 여과(percolate)하고, 값을 치환한다
  • 모든 항목에 대해 순회하며, $O(n \log n)$ 정렬을 하게 된다
• 이 정렬의 좋은 특징은,
  • 새로 추가될 항목들이 0번 인덱스의 요소를 이기지 않는다면(not better), 정렬을 진행하면서 그 새로운 항목들을 효과적으로 삽입할 수 있다
  • 또한 다음과 같은 시뮬레이션 컨텍스트(스케쥴링)에서 유용하다
    • 트리가 모든 이벤트를 가지고 있고,
    • 승리 조건이 가장 작게 예약된 시간(smallest scheduled time)인 경우
  • 어떤 이벤트가 실행을 위해 다른 이벤트를 예약(schedule)할 때, 그 이벤트는 미래에 예약되므로, 쉽게 힙에 들어갈 수 있다
  • 따라서 힙은 스케쥴러 구현하기에 좋은 구조
• 스케쥴러 구현 위한 다양한 구조가 연구 됐지만, 힙은 스케쥴에 좋고, 합리적으로 빠르며, 속도는 거의 상수 시간 속도이며, 최악의 경우에도 평균 케이스와 크게 다르지 않다.(하지만 전체적으로 더 효과적이지만, 최악의 경우 끔찍한 것들도 있다)
• 큰 디스크 정렬에도 매우 유용하다
  • 큰 정렬은, 미리 정렬된 시퀀스(크기는 CPU 메모리의 양과 관연 있음)인 “실행들(runs)” 생성을 의미
  • 그리고 실행들을 병합
  • 첫 정렬에서 가능한 가장 긴 runs를 생성하는 것이 매우 중요하며, 토너먼트가 이에 좋다
• 큰 정렬은 아래와 같이 여러 PASS와 runs로 구성

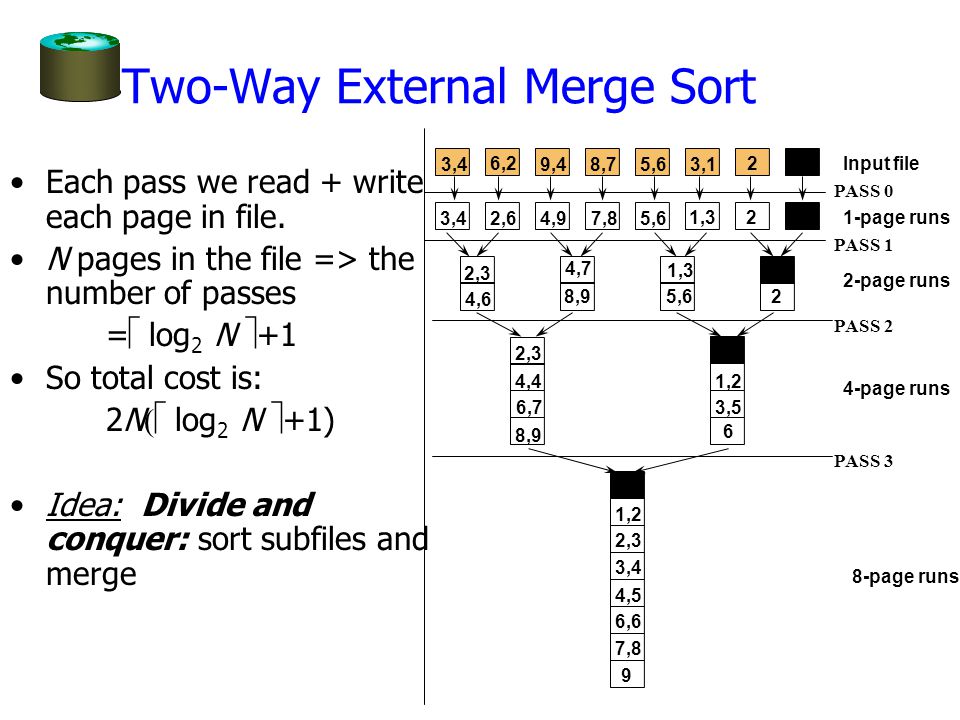
heapq의 함수들

heapq.py의 heappush

def heappush(heap, item):
    """Push item onto heap, maintaining the heap invariant."""
    heap.append(item)
    _siftdown(heap, 0, len(heap)-1)

# `heap`: 모든 인덱스가 `startpos`보다 크거나 같은 heap
# `pos`: 정리되지 않은(out-of-order) 값을 가질 가능성 있는 리프 노드
# 힙의 invariant 복구
def _siftdown(heap, startpos, pos):
    newitem = heap[pos] # 새로운 항목은 heap.append()로 항상 끝에 추가된다
    # 끝에서 루트까지, 새로운 항목이 들어 맞는 위치를 찾을 때까지 부모를 찾아 간다
    while pos > startpos:
        # k는 2*k+1과 2*k+2의 부모
        # 즉, 0은 1,2, 1은 3,4, 2는 5,6의 부모로, 리프 노드에서 부모를 찾으려면
        # (자식 인덱스 - 1)을 1비트 우로 움직여서 2로 나눈다
        parentpos = (pos - 1) >> 1 
        parent = heap[parentpos]
        if newitem < parent: # 새로운 항목이 기존의 부모 값보다 작다?
            heap[pos] = parent # 부모 값을 자식 위치로 보내고
            pos = parentpos # 다음 위치를 부모 인덱스로 변경한다
            continue
        break
    heap[pos] = newitem

• heap에 새로운 항목을 추가하고, 재탐색하여 힙의 불변성을 복원
• 부모 값이 더 크면 부모 값을 자식으로 보내고, 자식의 pos를 계속 찾아 올라간다

heappush(heap, 3)
# [3]
heappush(heap, 4)
# [3, 4]
heappush(heap, 5)
# [3, 4, 5]
heappush(heap, 6)
# [3, 4, 5, 6]
heappush(heap, 2)
# [3, 4, 5, 6, 2] heap 끝에 새로운 항목 추가
# [3, 4, 5, 6, 4] ((5-1)-1)/2=부모 위치=1. heap[1]=4. 4가 더 크므로 자식 위치로 보낸다. 2는 미정.
# [3, 3, 5, 6, 4] while문 돌아서 pos는 1, 부모는 0, a[0]=3 < 2이므로 a[1]=3으로 치환. 2는 미정.
# [2, 3, 5, 6, 4] while문 돌아서 pos는 0, 부모는 0, while문 종료, a[0]=2
""" 
      2
  3      5
6   4
"""
heappush(heap, 1)
# [2, 3, 5, 6, 4, 1]
# [2, 3, 5, 6, 4, 5]
# [2, 3, 2, 6, 4, 5]
# [1, 3, 2, 6, 4, 5]
"""
      1
  3       2
6   4   5 
"""

• 즉 해시 테이블처럼, 일정한 규칙에 따라 1차원 배열에서 부모 인덱스를 빠르게 찾아 값을 지환해 나간다
• 하지만 상위 cell이 하위 cell보다 작다는 것을 보장할 뿐, 상위 셀 하나와 하위 셀 둘 사이의 순서는 보장되지 않는다