ch19 Bit Manipulation

7 minute read

ch19 Bit Manipulation

비트 조작 개요

  • 1937년 클로드 섀넌(Claude Shannon)의 스위칭 회로 연구 $\to$ true, false 두 값으로 논리 연산 설명하는 부울 대수(Boolean Algebra) $\to$ 논리 게이트(Logic Gate) $\to$ 논리 회로(Logic Circuit) $\to$ 디지털 컴퓨터의 기본 개념이자 근간을 이룸

부울 연산자

NOT

X NOT X
false true
true false 
print("not True: {}".format(not True))  # -2: True는 1로 간주, -1 -1 = -2
print("not False: {}".format(not False))  # -1: False는 0으로 간주, 0 - 1 = -1
  • NOT = 2의 보수 - 1 $\to$ NOT x = -x - 1

AND

X Y X AND Y
false false false
false true false
true false false
true true true 
print("True and True: {}".format(True and True))
print("True and False: {}".format(True and False))
print("False and True: {}".format(False and True))
print("False and False: {}".format(False and False))

OR

X Y X OR Y
false false false
false true true
true false true
true true true 
print("True or True: {}".format(True or True))
print("True or False: {}".format(True or False))
print("False or True: {}".format(False or True))
print("False or False: {}".format(False or False))

XOR

X Y X OR Y
false false false
false true true
true false true
true true false
  • 하나가 true, 하나가 false인 경우에만 true가 된다
# and와 or를 조합하여 xor 구현
# (X and not Y) or (Y and not X)
# 1. X 또는 Y 두 변수 중 하나를 NOT 연산 후 AND 연산
# 2. 둘 중 하나라도 결과 True면 XOR에서 True
print("(True and not True) or (not True and True): {}".format((True and not True) or (not True and True)))
print("(True and not False) or (not True and False): {}".format((True and not False) or (not True and False)))
print("(False and not True) or (not False and True): {}".format((False and not True) or (not False and True)))
print("(False and not False) or (not False and False): {}".format((False and not False) or (not False and False)))

비트 연산자(Bit Operator)

비트 연산자 ~

print("~ True: {}".format(~ True)) # -2
print("~ False: {}".format(~ False)) # -1
  • True는 1로 간주되어 -2가 된다. 왜?
    • NOT = 2의 보수 - 1 $\to$ NOT x = -x - 1
    • $\text{NOT } x = -x -1$이 된다

비트 연산자 &

print("True & True: {}".format(True & True))
print("True & False: {}".format(True & False))
print("False & True: {}".format(False & True))
print("False & False: {}".format(False & False))

비트 연산자 |

print("True | True: {}".format(True | True))
print("True | False: {}".format(True | False))
print("False | True: {}".format(False | True))
print("False | False: {}".format(False | False))

비트 연산자 ^

print("True ^ True: {}".format(True ^ True))
print("True ^ False: {}".format(True ^ False))
print("False ^ True: {}".format(False ^ True))
print("False ^ False: {}".format(False ^ False))

print("True is not True: {}".format(True is not True))
print("True is not False: {}".format(True is not False))
print("False is not True: {}".format(False is not True))
print("False is not False: {}".format(False is not False))

비트 조작 퀴즈

비트 조작 +

print("bin(0b0110 + 0b0010) = bin({} + {}) = {} = {}".format(0b0110, 0b0010, bin(0b0110 + 0b0010), 0b0110 + 0b0010))
# bin(0b0110 + 0b0010) = bin(6 + 2) = 0b1000 = 8

비트 조작 *

print("bin(0b0011 * 0b0101) = bin({} * {}) = {} = {}".format(0b0011, 0b0101, bin(0b0011 * 0b0101), 0b0011 * 0b0101))
# bin(0b0011 * 0b0101) = bin(3 * 5) = 0b1111 = 15

비트 조작 >>

  • >> N은 N개의 비트를 우측으로 옮기고 $2^{N}$으로 나눈 몫과 같다
    • 당연하게도, N개의 비트를 버리고 남은 비트를 정수로 표현하기 때문
    • 1000에서 >> 2을 하면 10이 되며 이는 2가 되며, $\frac{8}{4}$와 같다
# 비트 두 개 우측으로 옮기므로 2^2로 나눈 것과 같다
print("bin(0b1101 >> 2) = bin({} >> 2) = {} = {}".format(0b1101, bin(0b1101 >> 2), 0b1101 >> 2))
# bin(0b1101 >> 2) = bin(13 >> 2) = 0b11 = 3

비트 조작 <<

  • << N은 N개의 비트를 좌측으로 옮기고 $2^{N}$으로 곱한 것과 같다
print("bin(0b1101 << 2) = bin({} << 2) = {} = {}".format(0b1101, bin(0b1101 << 2), 0b1101 << 2))
# bin(0b1101 << 2) = bin(13 << 2) = 0b110100 = 52

비트 조작 ~

  • 0b1100의 부정은 0b0011이 아닌 -0b1101이 된다. 왜?
    • NOT = 2의 보수 - 1 $\to$ NOT x = -x - 1
    • 0b1100 = 12
    • ~0b1100 = ~12 = -12 - 1 = -13
    • -13 = 1111 0011
    • 파이썬의 bin() 함수는 -(13) = -(0b1101) = -0b1101으로 나타낸다
print("bin(~0b1100) = {} = {}".format(bin(~0b1100), ~0b1100))
# bin(~0b1100) = -0b1101 = -13

비트 조작 ^

  • 0b0101 ^ ~0b1100 = 0b0101 ^ -0b1101 = 0b0101 ^ 1111 0011 = 1111 0110 = -10
EXPECTED ACTUAL
0b0101 0b0101
~0b1100 ~0b1100
0b0011 1111 0011
0b0110 1111 0110
6 -10 
print("bin(0b0101 ^ ~0b1100) = bin({} ^ {}) = bin({} ^ {}) = {} = {}".format(bin(0b0101), bin(~0b1100), 0b0101, ~0b1100, bin(0b0101 ^ ~0b1100), 0b0101 ^ ~0b1100))
# bin(0b0101 ^ ~0b1100) = bin(0b101 ^ -0b1101) = bin(5 ^ -13) = -0b1010 = -10

보수

  • 보수(complement)가 필요한 이유?
    • 보수를 이용하면 덧셈의 원리로 뺄셈이 가능하다
    • 즉, 가산기[+]로 모든 사칙 연산이 가능하며 감산기[-]가 불필요하다
  • 컴퓨터가 음수를 저장하기 위해 일반적으로 취하는 여러 방법 중 하나
  • 최상위 비트(MSB, Most Significant Bit)를 부호(sign) 비트로 사용

1의 보수

  • 음수 표현 시 $0 \to 1$로, $1 \to 0$으로 바꾼다

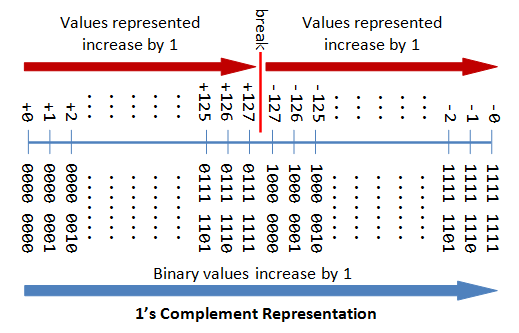
1_complement_1

  • 덧셈 시 순환 자리 올림(end around carry) 발생 가능 $\to$ 연산 시 올림수를 더해야 한다

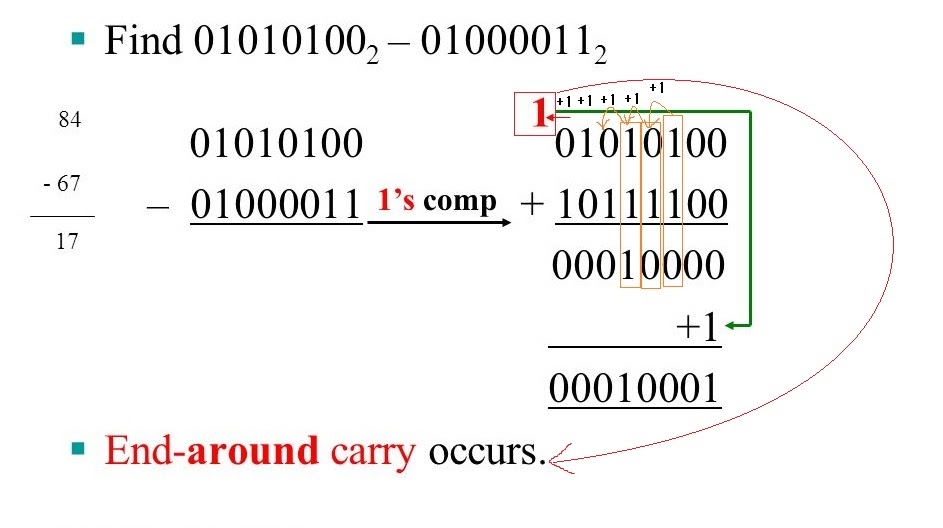
1_complement_2

84 - 67
  0101 0100
- 0100 0011

  0101 0100
+ 1011 1100 # 1의 보수
 10001 0000 # 순환 자리 올림수(end-around carry) 1이 생기면 다시 더한다

  0001 0000
+         1
  0001 0001 = 17
  • +와 -시 0과 1을 각각 치환하면 되는 점은 편하다
  • 하지만 +0과 -0이 생기고, 순환자리 올림수를 처리해야 한다는 단점이 있다

2의 보수

  • 2의 보수를 구하는 것과 NOT 연산을 혼동하지 말자
    • 2의 보수를 구하는 것: 비트를 뒤집고 +1하는 것
    • NOT 연산: NOT = 2의 보수 - 1 $\to$ NOT x = -x - 1
  • 2의 보수 표현과 연산
    • 표현:
      • 2의 보수 방식에 따라 숫자를 나타내는 것
      • 4비트에서 1000
        • 1000은 -8이 메모리에 저장되는 방식이다
        • 0111=7이며, NOT 7 = -7 - 1 = -8이 된다
    • 연산:
      • 보수 방식에 따라 실제 연산을 하는 것
      • 보수를 구하기 위해 비트 반전 후 +1
  • 2의보수와 NOT 연산을 정리하면 아래와 같을 듯 하다
  2의 보수 NOT
비트 연산 비트 반전 후 +1 2의 보수 - 1
10진수 표현   -x - 1

2의 보수 as 숫자 포맷

십진수 비트 비트 반전 후 +1    
0 0000 1111 + 1 0000 0
1 0001 1110 + 1 1111 -1
2 0010 1101 + 1 1110 -2
3 0011 1100 + 1 1101 -3
4 0100 1011 + 1 1100 -4
5 0101 1010 + 1 1011 -5
6 0110 1001 + 1 1010 -6
7 0111 1000 + 1 1001 -7
8 1000 0111 + 1 1000 -8
  • -8은?
    • 4비트 체계에서 첫 비트가 부호 비트로, 1이면 음수 의미
    • 1000은 8인데, 음수이므로 -8이 된다
    • 따라서 4비트 체계인 경우 8이 없다
    • 8비트 체계라면?
      • 0000 1000 = 8이 되고, 1111 1000 = -8이 된다
  • python에서 2의 보수를 표현하려면? 비트 마스크 사용
MASK = 0xF # 15 = 1111
print("bin(1 & MASK) = {}".format(bin(1 & MASK)))
print("bin(7 & MASK) = {}".format(bin(7 & MASK)))
print("bin(-8 & MASK) = {}".format(bin(-8 & MASK)))
print("bin(-7 & MASK) = {}".format(bin(-7 & MASK)))
print("bin(-1 & MASK) = {}".format(bin(-1 & MASK)))
"""
bin(1 & MASK) = 0b1
bin(7 & MASK) = 0b111
bin(-8 & MASK) = 0b1000
bin(-7 & MASK) = 0b1001
bin(-1 & MASK) = 0b1111
"""

2의 보수 as 수학 연산

  • 2의 보수 수학 연산
    • 가산 역 연산(Additive Inerse Operation)
    • 양수를 음수로, 음수를 양수로 바꾸는 작업
  • $1 \to 0$ 또는 $0 \to 1$로 비트를 뒤집은 후 비트에 +1을 해준다
  • 오버플로우?
    • n 비트 데이터에 대한 연산 결과를 n 비트로 나타낼 수 없을 때 발생
    • 부호 있는 4비트는 $-2^{4-1} \text{\textasciitilde} 2^{4-1} - 1 = -8 \text{\textasciitilde} 7$이므로, 이 범위를 벗어나는 수는 표현할 수 없게 된다
예제1: 0111 = 7
  • 4비트 체계인 경우
0111의 2의 보수 연산
   
  0111 = 7
비트 반전 1000
+1 1001
  -7
1001의 NOT연산
  • NOT = 2의 보수 - 1 $\to$ NOT x = -x - 1
   
  1001 = -7
NOT ~1000
  0111
-1 0110
  6

NOT 1000 = ~1000 = -x(비트 반전) -1 = 0111 -1 = 0110 = 6

예제2
  • NOT = 2의 보수 - 1 $\to$ NOT x = -x - 1
  • 1 = 0001의 2의 보수는 1110 + 1 = 1111 = -1

비트 연산자 NOT

  • NOT = 2의 보수 - 1 $\to$ NOT x = -x - 1
    • 비트 내에서 0과 1을 바꿔준다
    • -1을 한다
  • 4비트 체계에서 ~0111을 다시 보자면 아래와 같다
절차 내용
  7
  0111
NOT ~0111
0111의 2의 보수 1000 + 1
2의 보수 - 1 1000 + 1 - 1
  1000
10진수로 나타내기 1000
  -x -1
  -7 -1
  -8 
  0000 0101
^~0000 1100

# 먼저 NOT 연산
~0000 1100
 1111 0011

# 1111 0011을 십진수로 나타내면?
NOT x = -x - 1
NOT 12 = -12 - 1 = -13

# 다시 XOR 연산으로 돌아가면
 0000 0101
^1111 0011
 1111 0110

# 1111 0110을 십진수로 나타내면?
NOT x = -x - 1
x = 0000 1001 = 9
NOT 9 = -9 - 1 = -10

Updated:

You May Also Enjoy

Generator and yield

2 minute read

Generator and yield 개요 Generator? 관련 파일 async 함수와의 관계? ...

Plus Minus

1 minute read

Plus Minus 문제 조건 예제 해결 1st 1st 코드 나눗셈 함수 문제 풀이 코드 ...

A Very Big Sum

1 minute read

A Very Big Sum 문제 조건 예제 해결 1st 1st 코드 나눗셈 함수 ...