509 Fibonacci Number

• 509 Fibonacci Number
  • 문제
    • 피보나치 수열
  • 조건
  • 예제
  • 해결
    • 1st
      • 1 생각
      • 1 코드
      • 1 결과
        • fib_bottom_up
        • fib_top_down
    • 2nd 다른 풀이
      • 2 코드
      • 2 속도 비교

509 Fibonacci Number

문제

The Fibonacci numbers, commonly denoted F(n) form a sequence, called the Fibonacci sequence, such that each number is the sum of the two preceding ones, starting from 0 and 1. That is,
F(0) = 0, F(1) = 1
F(n) = F(n - 1) + F(n - 2), for n > 1.
Given n, calculate F(n).

• 각 수가 앞선 두 수의 합으로 이루어짐
• 0과 1부터 시작

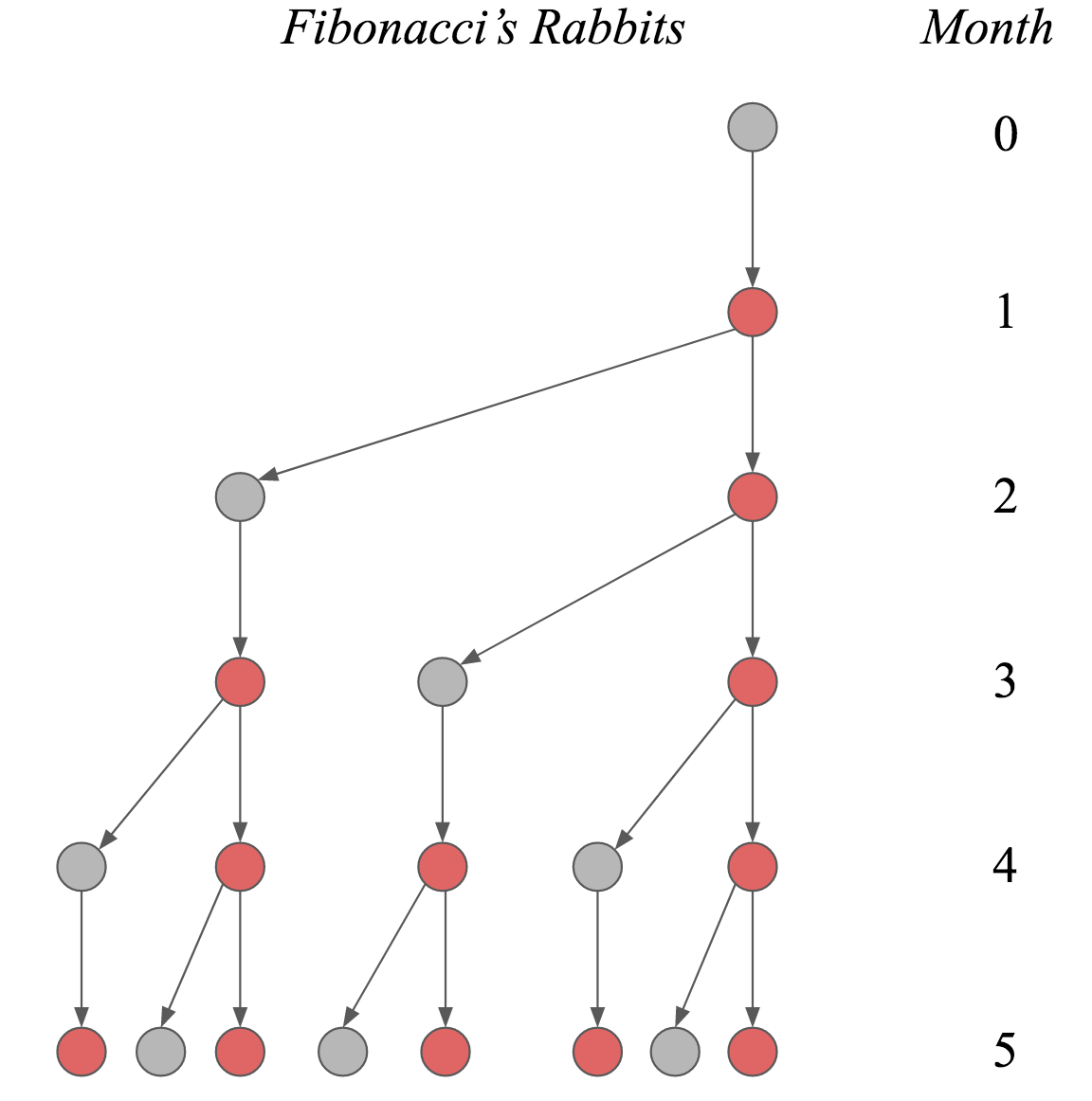
피보나치 수열

문제: 토끼가 한 쌍 있다면 몇 달이 지난 후에 토끼는 몇 쌍으로 늘어날까?
조건:

• 처음 토끼 한 쌍이 있으면 모든 쌍은 항상 한 배에 암수 한 쌍을 낳는다.
• 토끼 암컷은 태어난 지 한 달이면 새끼를 낳을 수 있으며, 계속하여 한 달에 함수 한 쌍씩 낳는다.
• 토끼는 죽지 않는다

조건

• 0 <= n <= 30

예제

Input: n = 2
Output: 1
Explanation: F(2) = F(1) + F(0) = 1 + 0 = 1.

Input: n = 3
Output: 2
Explanation: F(3) = F(2) + F(1) = 1 + 1 = 2.

Input: n = 4
Output: 3
Explanation: F(4) = F(3) + F(2) = 2 + 1 = 3.

해결

1st

1 생각

• 동적 계획법 상향식/하향식 모두 풀이를 해보자

1 코드

class Solution:
    dp = collections.defaultdict(int)

    def fib(self, n: int) -> int:
        return self.fib_bottom_up(n)

    # Tabulation
    def fib_bottom_up(self, n):
        self.dp[0] = 0
        self.dp[1] = 1

        for i in range(2, n + 1):
            self.dp[i] = self.dp[i - 1] + self.dp[i -2]

        return self.dp[n]

    # Memoization
    def fib_top_down(self, n):
        if n <= 1:
            return n
        
        if n in self.dp:
            return self.dp[n]
        
        self.dp[n] = self.fib_top_down(n - 1) + self.fib_top_down(n - 2)

        return self.dp[n]

1 결과

fib_bottom_up

Runtime: 24 ms, faster than 92.41% of Python3 online submissions for Fibonacci Number.
Memory Usage: 14.2 MB, less than 69.17% of Python3 online submissions for Fibonacci Number.

fib_top_down

Runtime: 44 ms, faster than 27.70% of Python3 online submissions for Fibonacci Number.
Memory Usage: 14 MB, less than 97.42% of Python3 online submissions for Fibonacci Number.

2nd 다른 풀이

2 코드

def fib_two_var(self, n):
    # x: 현재 피보나치 수
    # y: 다음 피보나치 수
    x, y = 0, 1
    for i in range(0, n):
        x, y = y, x + y
    return x

def fib_matrix(self, n):
    import numpy as np
    M = np.matrix([[0, 1], [1, 1]])
    vec = np.array([[0], [1]])

    return np.matmul(M ** n, vec)[0]

• 행렬 관련 참고1
• 행렬 관련 참고2

2 속도 비교

print('fib_bottom_up:{}'.format(timeit.timeit(lambda: s.fib_bottom_up(30), number=10000)))
print('fib_top_down:{}'.format(timeit.timeit(lambda: s.fib_top_down(30), number=10000)))
print('fib_two_var:{}'.format(timeit.timeit(lambda: s.fib_two_var(30), number=10000)))
print('fib_matrix:{}'.format(timeit.timeit(lambda: s.fib_matrix(30), number=10000)))

'''
fib_bottom_up:0.060466000000000006
fib_top_down:0.0042472999999999955
fib_two_var:0.01861639999999999
fib_matrix:0.6557445000000001
'''
 
""" import cProfile
import pstats
pr = cProfile.Profile()
pr.enable()
for i in range(10000):
    # s.fib_bottom_up(30)
    # s.fib_top_down(30)
    s.fib_two_var(30)
    # s.fib_matrix(30)
pr.disable()
pstats.Stats(pr).print_stats() """