2 Representing and Manipulating Information
2 정보의 표현과 조작(Representing and Manipulating Information)
2.0 개요
2.0.1 이진 수
- 컴퓨터는 두 개의 값으로 된 신호(two-valued signal = binary digit = bits)로 표현되는 정보를 저장하고 처리
- 두 개의 값으로 된 신호를 저장하고 연산하는 것은 매우 간단 $\to$ 수백만, 수십억의 회로를 단일 실리콘 칩에 집적 가능
- 해석(interpretation): bits를 묶어서 가능한 서로 다른 비트 패턴에 의미를 부여 $\to$ 비트 패턴으로 유한 집합의 요소들을 나타낼 수 있다
- 비트 묶음(groups of bits)을 사용하여 양의 숫자를 인코딩 가능
- 표준 문자 코드 사용하여 문서의 문자와 기호들을 인코딩 가능
2.0.2 세 가지 가장 중요한 숫자 표현
- 부호 없는(Unsigned) 수: 전통적인 이진 표기법에 기반하여 0보다 크거나 같은 숫자를 표현
- 2의 보수(Two’s-complement): 부호 있는(signed) 음과 양의 정수를 표현하는 가장 흔한 인코딩 방법
- Floating-point: 밑수(
base)를 2(base-2, 이진수)로 실수(real numbers)를 나타내는 과학적 표기법
2.0.3 overflow
- 컴퓨터는 제한된 수의 비트로 숫자를 표현하므로, 결과가 나타내기에 너무 크면 발생
- 정수 연산의 경우, 32비트 컴퓨터에서, $200 \times 300 \times 400 \times 500$는 $-884,901,888$이 된다
2.0.4 정수 연산과 실수 연산
- 정수 연산의 경우 $200 \times 300 \times 400 \times 500$가 $-884,901,888$ 되는 것은 비정상
- 여러 양의 수를 곱해 음수를 결과 $\to$ 정수 산술 연산의 속성에 반한다(run counter to)
- 하지만 그 와중에도 결합법칙(associative)과 교환법칙(commuative)은 만족
- 반면 실수 연산의 경우,
- 여러 양의 수를 곱하면 언제나 양수의 결과가 나온다. $+\infin$ 같은 특별한 값이 나오기도 하지만.
- 또한 한정된 정확도 표현으로 인해, 결합법칙(associative)가 적용되지 않는다
- 가령 $(3.14+1\mathrm{e}{20})-1\mathrm{e}{20} = 0.0$이 되지만, $3.14 + (1\mathrm{e}{20}-1\mathrm{e}{20}) = 3.14$가 된다
- 정수 산술 연산과 부동소수점 산술 연산이 다름은 표현의 한계를 어떻게 다루는가에 유래한다
- 정수 표현: 비교적 적은 범위의 값을 인코딩할 수 있지만 정확하다
- 실수 표현: 비교적 넓은 범위의 값을 인코딩할 수 있지만 대략적이다
2.0.5 정보 표현을 배우는 목적
- 실제 숫자를 표현하는 것에 대해 배움으로써
- 나타낼 수 있는 값의 범위를 이해하고
- 서로 다른 산술 연산의 속성을 이해
- 그렇다면 표현 가능한 값의 범위를 이해하고 서로 다른 산술 연산의 속성을 이해하는 것은 왜 중요할까?
- 모든 범위의 숫자 값에 대해 올바르게 작동하는 프로그램 작성에 중요
- 다양한 머신, OS 그리고 컴파일러 조합에 이식(portable)될 수 있는 프로그램 작성에 중요
- 또한 이러한 컴퓨터 연산의 미묘함(subtleties) 때문에 다수의 컴퓨터 보안 취약점 발생
- 비트 단위로 표현된 숫자들을 직접 조작한 산술 연산 이해 $\to$ 산술 연산 식 평가(arithmetic expression evaluation)의 성능을 최적화하기 위해 컴파일러에 의해 생성된 기계 레벨의 코드 이해에 중요
- C와 C++에서는 숫자 표현과 연산이 같지만, Java 언어에서는 숫자 표현과 연산에 대한 새로운 표준 집합 생성
- Java와 C 비교
Java built-in types are of a specified size and range defined by the language specification. In C++, a minimal range of values is defined for built-in types, but the exact representation (number of bits) can be mapped to whatever native types are preferred on a given platform.
- For instance, Java characters are 16-bit Unicode characters, and strings are composed of a sequence of such characters. C++ offers both narrow and wide characters, but the actual size of each is platform dependent, as is the character set used. Strings can be formed from either type.
- This also implies that C++ compilers can automatically select the most efficient representation for the target platform (i.e., 64-bit integers for a 64-bit platform), while the representation is fixed in Java, meaning the values can either be stored in the less-efficient size, or must pad the remaining bits and add code to emulate the reduced-width behavior.
2.1 정보 저장
2.1.0 개요
2.1.0.1 용어
- 8 bits(또는 bytes) 블록: 메모리의 주소 지정 가능한(addressable) 가장 작은 단위
- virtual memory: 기계 레벨의 프로그램은 메모리를 아주 큰 바이트 배열로 보며, 이를 가상 메모리라 한다
- address: 메모리의 각 바이트를 가리키는 유니크한 숫자
- virtual address space:
- 모든 가능한 주소의 집합
- 이름에서 알 수 있듯이, 기계 레벨 프로그램에 표시되는 개념적인 이미지이며, 실제로는 DRAM, flash memory, 디스크, 특별한 하드웨어 그리고 OS의 조합을 사용하여 단일(monolithic) 바이트 배열로 보이는 프로그램을 제공
2.1.0.1 저장
- 컴파일러와 런타임 시스템은 서로 다른 program obejct(또는 프로그램 데이터, 명령어, 그리고 제어 정보)를 저장하기 위해 메모리 공간을 보다 다루기 쉬운(more managable) 단위로 나눈다
- 프로그램의 서로 다른 부분들을 저장소에 저장하고 관리하기 위해 다양한 메커니즘 사용하며, 이러한 관리 작업들은 모두 가상 주소 공간에서 수행된다
- 예를 들어, C에서 포인터의 값은 저장소 블록의 첫 바이트의 가상 주소
- 또한 C 컴파일러는 type 정보를 각 포인터와 연관시 $\to$ 값의 타입에 따라 포인터가 가리키는(designated) 위치의 값에 접근할 수 있는 서로 다른 기계 레벨의 코드를 생성 가능
C에서 포인터의 역할? 배열을 포함한 데이터 구조의 요소(elements)를 참조하기 위한 메커니즘을 제공. 변수와 마찬가지로, 포인터는 value와 type이라는 두 측면을 갖는다.
- value: 어떤 오브젝트의 위치를 가리킨다
- type: 그 위치에 어떤 타입(예를 들어 정수 또는 실수)의 데이터가 저장되었는지 가리킨다
포인터를 제대로 이해하려면 포인터가 기계 레벨에서 어떻게 표현되고 구현되는지 확인할 필요가 있다.
2.1.1 16진수 표기법
- 8bits는 2진과 10진으로 아래와 같이 나타낼 수 있다
- 2진 표기법: $0000 0000_2 \sim 1111 1111_2$ 범위로 나타낼 수 있다
- 10진 표기법: $0_2 \sim 255_1$
- 하지만 2진, 10진 표기법은 비트 패턴을 나타내기에 그렇게 편하지 않다. 왜?
- 이진 표기법은 너무 장황하고
- 10진 표기법은 비트 패턴으로 바꾸거나 비트 패턴에서 10진수로 바꾸기 지겹다(tedious)?
- 대신 $0 \sim 9$의 숫자와 $A \sim F$ 문자를 사용하여 16개의 값을 나타낼 수 있는 16진수 사용
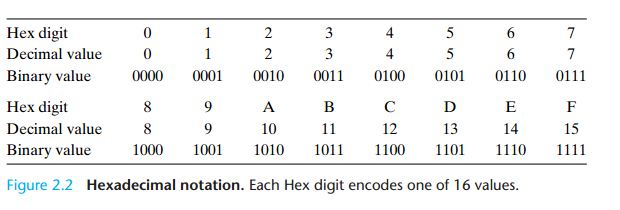
- 기계 레벨의 프로그램에서 가장 흔한 작업은 비트 패턴의 10진, 2진, 16진 표현을 변환하는 것
hex 1 7 3 A 4 C
bin 0001 0111 0011 1010 0100 1100
연습 문제 2.1
- A. 0x25B9D2를 이진수로 변환
- B. 1010111001001001를 16진수로 변환
- C. 0xA8B3D를 이진수로 변환
- D. 1100100010110110010110를 16진수로 변환
#include <stdio.h>
#include <math.h>
#include <string.h>
#include <stdlib.h>
int get_char_length(char arr[]){
int length;
for (length = 0; arr[length] != '\0'; ++length);
return length;
}
void print_buf(char *buf, int length) {
for(int k = length - 1; k >= 0; k--) {
printf("%d", buf[k]);
if(k % 4 == 0) {
printf(" ");
}
}
printf("\n");
}
// https://stackoverflow.com/a/26615844
int hexadecimal_to_binary(char hex[], char *buf) {
int i;
int decimal = 0;
int length = get_char_length(hex);
// 16진수를 10진수로 변환
for (i = 0; hex[i] != '\0'; ++i, --length) {
if(hex[i] >= '0' && hex[i] <= '9') {
decimal += (hex[i] - '0') * pow(16, length - 1);
}
if(hex[i] >= 'A' && hex[i] <= 'F') {
// printf("%c(%d): %d - %d\n",hex[i], hex[i], hex[i] - 'A', 'A');
// 'A' = 65, 하지만 16진수에서 A는 10이어야 하므로 55를 뺀다
decimal += (hex[i] - ('A' - 10)) * pow(16, length - 1);
}
if(hex[i] >= 'a' && hex[i] <= 'f') {
decimal += (hex[i] - ('a' - 10)) * pow(16, length - 1);
}
}
int j = 0;
// 10진수를 2진수로 변환
while (decimal != 0) {
// 0번 인덱스부터 채워넣는다
buf[j++] = decimal % 2;
decimal /= 2;
}
print_buf(buf, j);
return j;
}
// https://stackoverflow.com/a/5307692
int binary_to_hexadecimal(char bin[], char *buf) {
int num = 0;
// bin의 메모리 위치
char * tmp = bin;
// bin의 메모리 위치
char * a = tmp;
do {
int b = *a == '1' ? 1 : 0;
// printf("tmp: %d, a: %d, (%d << 1) | %d: %d\n", tmp, a, num, b, (num << 1) | b);
// 1비트씩 앞으로 밀어내고, 그 다음 0 또는 1인 b 비트를 합쳐 나간다. 이렇게 간단해지네...
num = (num << 1) | b;
a++;
} while (*a);
// https://stackoverflow.com/a/14733875 hex 출력
printf("0x%08X\n", num);
return 0;
}
int main() {
char bin[100];
char buf[100];
char hex[100];
int result;
strcpy(hex, "0x25B9D2");
result = hexadecimal_to_binary(hex, buf); // 10 0101 1011 1001 1101 0010
strcpy(bin, "1010111001001001");
result = binary_to_hexadecimal(bin, buf); // 0x0000AE49
strcpy(hex, "0xA8B3D");
result = hexadecimal_to_binary(hex, buf); // 1010 1000 1011 0011 1101
strcpy(bin, "1100100010110110010110");
result = binary_to_hexadecimal(bin, buf); // 0x00322D96
return 0;
}
정수 to 이진수
- $n$이 양수인 $x = 2^n$에 대하여, $x$는 간단하게 1과 n개의 0으로 나타낼 수 있다
2의 거듭제곱 $\to$ 16진수
- 16진수에서 0은 2진수로 0000을 의미
- $0 \le i \le 3$인 $n = i + 4j$에 대하여, $x$는 $1{(i=0)}, 2{(i=1)}, 4{(i=2)}, 8{(i=3)}$과 j개의 0으로 나타낼 수 있다
연습 문제 2.2:
| n | $2^n$ (정수) | $2^n$(16진수) |
|---|---|---|
| 5 | 32 | 0x20 |
| 23 | 8,388,608 | $23 = 3 + (4 \times 5) \to$ 0x800000 |
| 15 | 32,768 | $15 = 3 + (4 \times 3) \to$ 0x8000 |
| 13 | 8,192 | 0x2000 = $1 + (4 \times 3) = 13 = n$ |
| 12 | 4,096 | $12 = 0 + (4 \times 3) \to$ 0x1000 |
| 6 | 64 | $6 = 2 + (4 \times 1) to$ 0x40 |
| 8 | 256 | 0x100 = $0 + (4 \times 2) = 8$ |
정수 $\to$ 16진수
- 정수 $x$를 16으로 계속 나눠서 지수(quotient) $q$와 나머지 $r$을 구한다
- $q$
- $r$: 최소 유효 숫자(least significant digit), 즉 0부터 F까지 16진수로 나타낼 수 있는 수
\(x = (q \cdot 16) + r\) \(314,156 = 19,634\cdot 16 + 12 = C\) \(119,634 = 1,227\cdot 16 + 2 = 2\) \(1,227 = 76\cdot 16 + 11 = B\) \(76 = 4\cdot 16 + 12 = C\) \(4 = 0\cdot 16 + 4 = 4\) \(0x4CB2C\)
16진수 $\to$ 정수
- 반대로 16을 계속 곱한다
\(7\cdot 16^2 + 10\cdot 16^1 + 15\) \(7\cdot 256 + 10\cdot 16^1 + 15\) \(1,792 + 160 + 15\) \(1,967\)
연습 문제 2.3: 단일 바이트는 2 개의 16진수로 표현될 수 있다(8비트니까)
| decimal | binary | hexadecimal |
|---|---|---|
| 0 | 0000 0000 | 0x00 |
| 158 | $2^7 + 2^4 + 2^3 + 2^2 + 2 =$ 1001 1110 | $16 \cdot 9 + 14$: 0x9E |
| 76 | $2^6 + 2^3 + 2^2 =$ 0100 1100 | $16 \cdot 4 + 12$: 0x4C |
| 145 | $2^7 + 2^4 + 2^0 =$ 1001 0001 | $16 \cdot 9 + 1$: 0x91 |
| 174 | 1010 1110 = $2^7 + 2^5 + 2^3 + 2^2 + 2^1$ | $16 \cdot 10 + 14$: 0xAE |
| 60 | 0011 1100 = $2^5 + 2^4 + 2^3 + 2^2$ | $16 \cdot 3 + 12$: 0x3C |
| 241 | 1111 0001 = $2^7 + 2^6 + 2^5 + 2^4 + 2^0$ | $16 \cdot 15 + 1$: 0xF1 |
- 정수에서 이진수, 2의 거듭제곱에서 16진수, 정수에서 16진수, 16진수에서 정수 변환의 관계는?
| Decimal | Binary | Hexadeciaml |
|---|---|---|
| $7 \times 16 + 5 \times 16^0 = 117$ | $2^6 + 2^5 + 2^4 + 2^2 + 2^0 =$0111 0101 | 0x75 |
| $\text{B(=11)} \times 16^1 + \text{D(=13)} \times 16^0 = 189$ | $2^7 + 2^5 + 2^4 + 2^3 + 2^2 + 2^0=$1011 1101 | 0xBD |
| $\text{F(=15)} \times 16^1 + 5 \times 16^0 = 245$ | $2^7 + 2^6 + 2^5 + 2^4 + 2^2 + 2^0=$1111 0101 | 0xF5 |
연습 문제 2.4: 숫자를 10진수 또는 2진수로 변환하지 않고 다음 산술 연산 시도. 힌트: 정수 덧셈과 뺄셈에 사용하는 방법만 수정. 어떻게??
- 10진수에서 덧셈은? 합이 10을 초과하면 자리수를 올린다
- 10 + 5 = 15
- 9 + 11 = 20
- 10진수에서 뺄셈은? 차가 10을 초과하면 자리수를 내린다
- 10 - 5 = 5
- 9 - 11 = -2
- A. 0x605c + 0x5
- c와 5를 합하면, D,E,F,0,1로 마지막 수는 1이 되고 자리수 올림
- = 0x6061
- B. 0x605c - 0x20
- 5c와 20을 빼면
- = 0x603c
- C. 0x605c + 32
- D. 0x60fa - 0x605c
- a와 c를 빼면? a가 더 낮은 수이므로 위의 자리수를 가져온다
- 16 + a - c = 14 = E
- 앞자리수를 가져왔으므로 0x60ee - 0x6050와 같다
- ee에서 50를 빼면 9e
- 0x9e
2.1.2 데이터 사이즈
word 사이즈
word size: 포인터 데이터의 nominal size(명목상의 크기)라는데, 명목상의 크기가 뭐지?- 어쨌든 32bit, 64bit 컴퓨터에서 32, 64가 word 크기를 의미
- 가상 주소는 이러한 word로 인코딩되므로, word 크기로 결정되는 가장 중요한 시스템 파라미터는 가상 주소 공간의 최대 크기
- w 비트 word 크기의 머신의 경우, 가장 주소 범위는 $0 \sim 2^{w} - 1$이며, 프로그램은 최대 $2^w$ 바이트 접근 가능하다
- 32bit word 크기에서는 가상 공간 크기가 4 GB($4 \times 10^9$ 약간 초과)
- 64bit word 크기에서는 가상 공간 크기가 16 exabytes(약 $1.84 \times 10^19$)
- exabyte = $10^{18}$
32bit 프로그램:- 32비트 머신에서 사용하기 위해 컴파일된 프로그램
- 32비트 및 64비트 머신에서 사용 가능
gcc -m32 prog.c
64bit 프로그램- 64비트 머신에서 사용하기 위해 컴파일된 프로그램
- 64비트에서만 사용 가능
gcc -m64 prog.c
- 컴파일러는 데이터 인코딩 위해 다양한 방식을 사용하는 여러 데이터 포맷(integer, float 등) 지원
기본 C 데이터 타입의 일반적인 크기
| Signed | Unsigned | 32-bit bytes | 64-bit bytes |
|---|---|---|---|
| [signed] char | unsigned char | 1 | 1 |
| short | unsigned short | 2 | 2 |
| int | unsigned | 4 | 4 |
| long | unsigned long | 4 | 8 |
| int32_t | uint32_t | 4 | 4 |
| int64_t | uint64_t | 8 | 8 |
| char * | 4 | 8 | |
| float | 4 | 4 | |
| double | 8 | 8 |
signed: 음수, 0, 양수 표현 가능unsigned: 음이 아닌 수 표현 가능char: 1 byteshort,int,long: 어떤 범위의 크기를 제공*: 포인터
T *p;에 대해, p는 포인터 변수이며, 타입이 T인 오브젝트를 가리킨다
char *p;에 대해, p는 포인터 변수이며, 타입이 char인 오브젝트를 가리킨다
2.1.3 Addressing and Byte Ordering
- 여러 바이트로 구성되는 프로그램 오브젝트에 대해, 반드시 두 가지 규칙(convention)을 세워야 한다
- 오브젝트의 주소는 어디에?
- 메모리에 byte를 어떤 순서로 정렬?
- 사실 모든 머신에서 multi-byte의 오브젝트는 일련의 연속된 바이트로 저장된다
- 최하위 비트(Least Significant Bit)부터 저장?
little-edian - 최상위 비트(Most Significant Bit)부터 저장?
big-edian
- 최하위 비트(Least Significant Bit)부터 저장?
- 최근 많은 마이크로프로세서 칩들이
big-edian이지만, 실제로는 특정 OS가 결정되면 바이트 정렬 방식은 고정된다
메모리에 byte를 정렬은 어떻게?
\[[x_{w-1}, x_{w-2}, \dotsb, x_1, x_0]\]- $x_0$: LSB(Least Significant Bit), 최하위 비트(bit)
- $x_{w-1}$: MSB(Most Significant Bit), 최상위 비트(bit)
- $w$: 8배수
- $[x_{w-1}, x_{w-2}, \dotsb, x_{w-8}]$: 최상위 바이트(byte, 8bit)
- $[x_{7}, x_{6}, \dotsb, x_{0}]$: 최하위 바이트(byte, 8bit)
little edian
# int 타입 변수 x는 0x100 주소에 16진수 0x01234567 값 가질 경우
0x100 0x101 0x102 0x103
...| 67 | 45 | 23 | 01 | ...
- 0x01234567에서 0x67이 하위(low order)
- 최하위 바이트부터 정렬
- 대부분의 인텔 호환 머신은
little-edian모드로만 작동
big edian
# int 타입 변수 x는 0x100 주소에 16진수 0x01234567 값 가질 경우
0x100 0x101 0x102 0x103
...| 01 | 23 | 45 | 67 | ...
- 0x01234567에서 0x01이 상위(high order)
- 최상위 바이트부터 정렬
- 대부분의 IBM과 Oracle 머신은
big-edian모드로 작동
바이트 정렬은 언제 중요할까?
네트워크로 서로 다른 머신 간 이진 데이터 통신 시
- 이 문제를 피하기 위해 전송 머신은 네트워크 표준에 따라 변환하여 전송하고
- 수신 머신은 네트워크 표준을 내부 방식으로 변환
정수 데이터를 나타내는 바이트 시퀀스
4004d3: 01 05 43 0b 20 00 add %eax,0x200b43(%rip)
- 머신 레벨 코드
- 일련의 16진수 바이트
01 05 43 0b 20 00:- 현재 program counter의 값에 0x200b43을 더하여 주소를 얻고
- 얻은 주소 위치에 저장된 값에
- 데이터(a word of data)를 더하라
- 마지막 4 bytes
43 0b 20 00에 대하여- 역순으로 적으면
00 20 0b 43이 되고 - 앞의 0을 제거하면
20 0b 43이 되어 우측 쓰여 있는0x200b43이란 값을 얻을 수 있다
- 역순으로 적으면
일반 시스템을 우회하는 프로그램
- C 언어에서
cast나union은 오브젝트 생성 시 데이터 타입과 다른 데이터 타입으로 참조될 수 있도록 한다
#include <stdio.h>
// typedef: 데이터 타입에 이름 부여 > 가독성 향상
typedef unsigned char *byte_pointer;
void show_bytes(byte_pointer start, size_t len) {
int i;
for (i = 0; i < len; i++)
printf(" %.2x", start[i]);
printf("\n");
}
void show_int(int x){
show_bytes((byte_pointer) &x, sizeof(int));
}
void show_float(float x){
show_bytes((byte_pointer) &x, sizeof(float));
}
void show_pointer(void *x){
show_bytes((byte_pointer) &x, sizeof(void *));
}
int main(){
show_int(1); // 01 00 00 00
show_float(2.0); // 00 00 00 40
return 0;
}
- 인자
x에 대한 포인터&x를unsigned cahr *타입으로 캐스팅((byte_pointer))하여 전달 - 이 캐스팅은 컴파일러에게 프로그램이 해당 포인터가 원래 데이터 타입의 오브젝트가 아닌
unsigned char로 봐야 한다는 것을 알려준다 sizeof(T)? 타입 T를 저장하기 위해 필요한 bytes의 수를 반환- 고정된 값이 아닌
sizeof사용? 서로 다른 머신 타입에 이식 가능한 코드 작성 위한 첫 단계
- 고정된 값이 아닌
- 서로 다른 머신에서 당야한 데이터 값들의 바이트 표현
| Machine | Value | Type | Bytes(hex) | edian |
|---|---|---|---|---|
| Linux32 | 12,345 | int | 39 30 00 00 | little |
| Wndows | 12,345 | int | 39 30 00 00 | little |
| Sun | 12,345 | int | 00 00 30 39 | big |
| Linux64 | 12,345 | int | 39 30 00 00 | little |
| Linux32 | 12,345.0 | float | 00 e4 40 46 | little |
| Wndows | 12,345.0 | float | 00 e4 40 46 | little |
| Sun | 12,345.0 | float | 46 40 e4 00 | big |
| Linux64 | 12,345.0 | float | 00 e4 40 46 | little |
| Linux32 | &ival | int* | e4 f9 ff bf | little |
| Wndows | &ival | int* | b4 cc 22 00 | little |
| Sun | &ival | int* | ef ff fa 0c | big |
| Linux64 | &ival | int* | b8 11 e5 ff ff 7f 00 00 | little |
- 정수와 부동 소수점 모두 12,345 숫자를 매우 다른 패턴으로 인코딩하지만, 바이너리 패턴으로 비교했을 때 13개의 비트가 매칭되며, 이는 우연이 아니다
0 0 0 0 3 0 3 9
0000 0000 0000 0000 0011 0000 0011 1001
| |||| |||| ||||
0100 0110 01 0000 0011 1001 00 0000 0000
4 6 4 0 E 4 0 0
연습 문제 2.5
다음과 같이 show_bytes를 세 번 호출한다고 했을 때, Little-edian과 Big-edian에서 출력되는 값은?
int a = 0x12345678;
byte_pointer ap = (byte_pointer) &a;
show_bytes(ap, 1); /* A. */
show_bytes(ap, 2); /* B. */
show_bytes(ap, 3); /* C. */
| size_t | Little | Big | |
|---|---|---|---|
| A | 1 | 78 | |
| B | 2 | 78 56 | |
| C | 3 | 78 56 34 |
연습 문제 2.6
정수 2,607,352는 16진수로 0x0027C8F8이며, 부동소수점 3,510,593.0은 16진수로 0x4A1F23E0이다.
- A. 두 수의 이진 표현 작성
0x0027C8F8:- 10 0111 1100 1000 1111 1000
- 1001111100100011111000
0x4A1F23E0:- 100 1010 0001 1111 0010 0011 1110 0000
- 1001010000111110010001111100000
- B. 매치되는 비트가 최대가 되도록 두 문자열을 이동시켰을 때, 얼마나 매치되는가? 20 개의 비트
2 7 C 8 F 8
1001 1111 0010 0011 1110 00
||| |||| |||| |||| |||| ||
100 1010 0001 1111 0010 0011 1110 0000
4 A 1 F 2 3 E 0
- C. 문자열의 어떤 부분이 매치되지 않는가? 최상위 비트 1
오브젝트 주소는 어디에?
2.1.4 문자열 표현
- C에서 문자열은
null로 종료되는 문자들의 배열로 인코딩 된다 - 각 문자는 ASCII 문자 코드 같은 표준으로 인코딩되어 표현된다
show_bytes("12345", 6)을 실행해 보면,31 32 33 34 35 00가 출력된다- 십진수 $x$는 ASCII 코드에서 0x3$x$가 되고, 종료 바이트(terminating byte)는 0x00으로 표현
- ASCII를 문자 코드로 사용하는 어떤 시스템에서든 같은 결과가 나오며, 바이트 정렬이나 워드 크기 규칙(convention)에 독립적이다
연습 문제 2.7
다음 show_bytes 호출하면 뭐가 출력되는가?a는 0x61,z는 0x7A다
const char *m = "mnopqr";
show_bytes((byte_pointer) m, strlen(m)); // 6d 6e 6f 70 71 72
2.1.5 코드 표현
- 아래 코드를 sum.c로 저장하고, main 함수 없이 컴파일 하면 sum.o 파일을 얻게 된다
int sum(int x, int y) {
return x + y;
}
gcc -c sum.c -lm
-rw-rw-r--. 1 aimpugn aimpugn 42 4월 2 22:56 sum.c
-rw-rw-r--. 1 aimpugn aimpugn 1240 4월 2 22:59 sum.o
- sum.o 오브젝트를 얻을 수 있고, 또는 -save-temps 옵션을 사용해서
.s,.o,.i파일을 얻을 수 있다
$ gcc -c -save-temps sum.c
$ ll
-rw-rw-r--. 1 aimpugn aimpugn 42 4월 2 22:56 sum.c
-rw-rw-r--. 1 aimpugn aimpugn 190 4월 2 23:03 sum.i
-rw-rw-r--. 1 aimpugn aimpugn 1240 4월 2 23:03 sum.o
-rw-rw-r--. 1 aimpugn aimpugn 450 4월 2 23:03 sum.s
$ cat sum.s
.file "sum.c"
.text
.globl sum
.type sum, @function
sum:
.LFB0:
.cfi_startproc
pushq %rbp
.cfi_def_cfa_offset 16
.cfi_offset 6, -16
movq %rsp, %rbp
.cfi_def_cfa_register 6
movl %edi, -4(%rbp)
movl %esi, -8(%rbp)
movl -4(%rbp), %edx
movl -8(%rbp), %eax
addl %edx, %eax
popq %rbp
.cfi_def_cfa 7, 8
ret
.cfi_endproc
.LFE0:
.size sum, .-sum
.ident "GCC: (GNU) 8.3.1 20191121 (Red Hat 8.3.1-5)"
.section .note.GNU-stack,"",@progbits
- 이에 대해
od로 16진수 byte로 출력을 해보면 다음과 같다
od -x -t c sum.s
0000000 2e09 6966 656c 2209 7573 2e6d 2263 090a
\t . f i l e \t " s u m . c " \n \t
0000020 742e 7865 0a74 2e09 6c67 626f 096c 7573
. t e x t \n \t . g l o b l \t s u
0000040 0a6d 2e09 7974 6570 7309 6d75 202c 6640
m \n \t . t y p e \t s u m , @ f
0000060 6e75 7463 6f69 0a6e 7573 3a6d 2e0a 464c
u n c t i o n \n s u m : \n . L F
0000100 3042 0a3a 2e09 6663 5f69 7473 7261 7074
B 0 : \n \t . c f i _ s t a r t p
0000120 6f72 0a63 7009 7375 7168 2509 6272 0a70
r o c \n \t p u s h q \t % r b p \n
0000140 2e09 6663 5f69 6564 5f66 6663 5f61 666f
\t . c f i _ d e f _ c f a _ o f
0000160 7366 7465 3120 0a36 2e09 6663 5f69 666f
f s e t 1 6 \n \t . c f i _ o f
0000200 7366 7465 3620 202c 312d 0a36 6d09 766f
f s e t 6 , - 1 6 \n \t m o v
0000220 0971 7225 7073 202c 7225 7062 090a 632e
q \t % r s p , % r b p \n \t . c
0000240 6966 645f 6665 635f 6166 725f 6765 7369
f i _ d e f _ c f a _ r e g i s
0000260 6574 2072 0a36 6d09 766f 096c 6525 6964
t e r 6 \n \t m o v l \t % e d i
0000300 202c 342d 2528 6272 2970 090a 6f6d 6c76
, - 4 ( % r b p ) \n \t m o v l
0000320 2509 7365 2c69 2d20 2838 7225 7062 0a29
\t % e s i , - 8 ( % r b p ) \n
0000340 6d09 766f 096c 342d 2528 6272 2970 202c
\t m o v l \t - 4 ( % r b p ) ,
0000360 6525 7864 090a 6f6d 6c76 2d09 2838 7225
% e d x \n \t m o v l \t - 8 ( % r
0000400 7062 2c29 2520 6165 0a78 6109 6464 096c
b p ) , % e a x \n \t a d d l \t
0000420 6525 7864 202c 6525 7861 090a 6f70 7170
% e d x , % e a x \n \t p o p q
0000440 2509 6272 0a70 2e09 6663 5f69 6564 5f66
\t % r b p \n \t . c f i _ d e f _
0000460 6663 2061 2c37 3820 090a 6572 0a74 2e09
c f a 7 , 8 \n \t r e t \n \t .
0000500 6663 5f69 6e65 7064 6f72 0a63 4c2e 4546
c f i _ e n d p r o c \n . L F E
0000520 3a30 090a 732e 7a69 0965 7573 2c6d 2e20
0 : \n \t . s i z e \t s u m , .
0000540 732d 6d75 090a 692e 6564 746e 2209 4347
- s u m \n \t . i d e n t \t " G C
0000560 3a43 2820 4e47 2955 3820 332e 312e 3220
C : ( G N U ) 8 . 3 . 1 2
0000600 3130 3139 3231 2031 5228 6465 4820 7461
0 1 9 1 1 2 1 ( R e d H a t
0000620 3820 332e 312e 352d 2229 090a 732e 6365
8 . 3 . 1 - 5 ) " \n \t . s e c
0000640 6974 6e6f 2e09 6f6e 6574 472e 554e 732d
t i o n \t . n o t e . G N U - s
0000660 6174 6b63 222c 2c22 7040 6f72 6267 7469
t a c k , " " , @ p r o g b i t
0000700 0a73
s \n
0000702
- 책에서는 OS별로 byte 표현이 다르다는 것을 보여주고 있다. 서로 다른 머신에서 서로 다르고 호환되지 않은 명령어와 인코딩을 사용하며, 같은 프로세서라도 OS가 다르면 그 시스템 자체적인 코딩 컨벤션이 있기 때문에 바이너리가 상호 호환되지 않는다.
| OS | |
|---|---|
| Linux32 | 55 89 e5 8b 45 0c 03 45 08 c9 c3 |
| Windows | 55 89 e5 8b 45 0c 03 45 08 c9 c3 |
| Sun | 81 c3 e0 08 90 02 00 09 |
| Linux62 | 55 48 89 e5 89 7d fc 89 75 f8 03 45 fc c9 c3 |
- 컴퓨터 시스템의 기본 개념(fundamental concept)은, 머신의 관점에서 프로그램이란 단순히 일련의 바이트라는 것.
- program = a sequence of bytes
2.1.6 불 대수(bool algebra) 소개
- 불 대수(bool algebra)?
- 어떤 명제의 참(true)과 거짓(false)를 1과 0에 대응 시켜서
- 명제와 명제 간의 관계를 수학적으로 표현